Árboles y Grafos

ÁRBOLES Y GRAFOS

Publicado por: Diego Valdez Martínez

Grafos 

Los grafos son estructuras discretas que aparecen ubicuamente en cada disciplina donde se requiere modelar algo. En general los grafos son mapas conceptuales que ayudan a representar el conocimiento. 
En este contexto árboles y grafos se refiere a estructuras de datos que permiten organizar y mantener información en un computador. Esta forma se inspira una forma de organizar información con lápiz y papel usando nodos y flechas entre los nodos (a esas flechas también se les llama arcos, a los nodos también se les llama vértices). Los grafos y árboles en papel son apropiados por ejemplo para capturar sólo una parte de la información de objetos, situaciones y otros tipos de información.

• Aplicaciones de los grafos: 

1. Internet y los protocolos de comunicaciones (TCP/IP, SMTP, FTP, routers, etc.) 
2. Diseño de redes de comunicaciones y transporte (redes computacionales, carreteras, aguas, electricidad, telecomunicaciones, aviación, satélites, aero-espacial, flotas de vehículos, etc.)
3. Estructura de datos 
4. Algoritmos computacionales  Navegador GPS (Google Maps)
5. Ocio (video juegos, simulación e IA) 
6. Domótica, robótica, automatización, control y gestión de redes, etc. 
7. La Web (es un grafo cuya estructura cambia cada segundo) 
8. Web semántica  Investigación médica, biogenética (secuenciación ADN) 
9. Biología, medio-ambiente, cambio climático 
10. Árboles genealógicos

Propiedades de los Grafos

• Adyacencia. Dos aristas son adyacentes si tienen un vértice en común, y dos vértices son adyacentes si una arista los une. 
• Incidencia. Una arista es incidente a un vértice si ésta lo une a otro. 
• Ponderación. Corresponde a una función que asocia a cada arista un valor (costo, peso, longitud, etc.), para aumentar la expresividad del modelo. 
• Etiquetado. Distinción que se hace a los vértices y/o aristas mediante una marca que los hace unívocamente distinguibles del resto.

¿Qué es un grafo? 

Un grafo G consiste en un conjunto no vacío de vértices o nodos V y un conjunto de arcos o aristas E G = (V,E). Grafo del griego grafos: dibujo, imagen.

Cada e є E tiene un par (v1 ,v2 ) є V x V asociado; es decir, e conecta v1 con v2 .

El orden del grafo G a su número de vértices  G = |V|.

El grado de un vértice o nodo v є V es igual al número de arcos o aristas que lo tienen como extremo.

Vértices (Nodos). Elementos (objetos) que forman un grafo. Cada uno lleva asociada un grado característico según la situación, que se corresponde con la cantidad de arcos o aristas que confluyen en dicho vértice. 

• Arcos o Aristas. Relaciones entre los elementos que forman el grafo. Existen los siguientes tipos: Ramas. Arco o arista que unen un vértice con otro. 
• Paralelas (múltiples). Arcos o aristas conjuntas si el vértice inicial y final son el mismo.
• Cíclicas (lazo, bucle). Arco o arista que el vértice inicial y final es el mismo. 

Un grafo ponderado G = (V,E,w) es un grafo en el que a cada arco o arista se le asocia un peso.

En un grafo dirigido, un vértices es adyacente a otro si están conectados por un arco (cola → cabeza), donde el vértice cabeza es adyacente al vértice cola. 

• En tal caso, el vértices cola es incidente al vértice cabeza. 

En un grafo no dirigido, dos vértices son adyacentes si están conectados por una arista. 

• En tal caso, cada uno de estos vértices es incidente a dicha arista. 

Un grafo dirigido o digrafo G consiste en un conjunto no vacío de vértices V y un conjunto de arcos E G = (V,E).  

• Los vértices se denominan también nodos o puntos. 
• Los arcos pueden llamarse arcos dirigidos o líneas dirigidas. 

Un arco es un par ordenado de vértices (v,w); donde v es la cola (nodo inicial) y w es la cabeza (nodo terminal) del arco. 

• El arco (v,w) se expresa a menudo como v → w, y se representa como:
• Se dice que el arco v → w va de v a w, y que w es adyacente o vecino a v. 
• Se dice que el arco v → w es incidente en el vértice v.

Cuando un arco es un par ordenado de vértices idénticos se llama lazo, bucle o arco cíclico, arco que une un vértice consigo mismo. 

• El lazo (v,v) se expresa a menudo como v → v, y se representa como:
• Se dice que el arco v → v va de v a v, y que v es adyacente a v.
• Se dice que el arco v → v es incidente en el vértice v.

El grado de entrada (interno) de v es el número de arcos que tienen como nodo terminal a v y se denota por g - (v).  El grado de salida (externo) de v es el número de arcos que tienen como nodo inicial a v y se denota por g+ (v).

ÁRBOLES

Los árboles representan las estructuras no-lineales y dinámicas de datos más importantes en computación. Dinámicas, puesto que a cada elemento del árbol pueden seguirlo varios elementos

PROPIEDADES DE UN ÁRBOL: En la ciencia de la computación definimos un árbol como un conjunto de nodos y líneas. Un nodo es un elemento de información que reside en el árbol. Una línea es un par de nodos ordenados, y a la secuencia de líneas se le denomina ruta. Además, los árboles tienen las siguientes propiedades:  Tienen un nodo al que se le llama raíz del árbol. 

• Todos los nodos, excepto la raíz, tienen una sola línea de entrada (el nodo raíz no tiene ninguna). 
• Existe una ruta única del nodo raíz a todos los demás nodos del árbol.
• Si hay una ruta <a,b>, entonces a „b‟ se le denomina “hijo” de “a” y es el nodo raíz de un subárbol.

Gráficamente puede representarse una estructura árbol de diferentes maneras y todas ellas equivalentes;
CARACTERISTICAS DE UN ÁRBOL: 

• NODO indica un elemento, o ítem, de información. 
• Todo árbol que no es vacío, tiene un único nodo raíz. 
• Un nodo X es descendiente directo de un nodo Y, si el nodo X es apuntado por el nodo Y. X es hijo de Y. 
• Un nodo X es antecesor directo de un nodo Y, si el nodo X apunta al nodo Y. X es padre de Y.
• Se dice que todos los nodos que son descendientes directos (hijos) de un mismo nodo (padre), son hermanos.
• Todo nodo que no tiene ramificaciones (hijos), se conoce con el nombre de terminal u hoja.
• Todo nodo que no es raíz, ni terminal u hoja se conoce con el nombre de interior. 8. Grado es el número de descendientes directos de un determinado nodo. Grado del árbol es el máximo grado de todos los nodos del árbol.
• Nivel es el número de arcos que deben ser recorridos para llegar a un determinado nodo. Por definición, la raíz tiene nivel 1.
• Altura del árbol es el máximo número de niveles de todos los nodos del árbol.

EJEMPLO DE UN ÁRBOL 

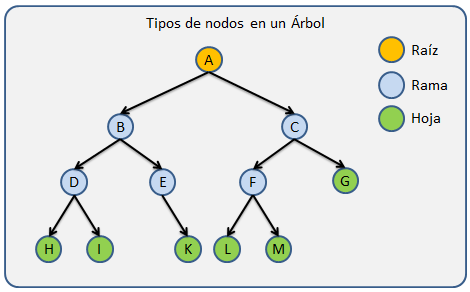
1. A es la raíz del árbol. 
2. B es hijo de A.
3. A es padre de B.
4. B y C son hermanos.
5. I,E,J,K,G,L son hojas.
6. B, D, F, C, H son nodos interiores.
7. El grado de nodo A es 2. 
8. Nivel del nodo A es 1.
9. Nivel B es 2.
10. Altura del árbol 4. 
11. A ED CB F G H I J K L

ÁRBOL BINARIO: Un árbol ordenado es aquel en el cual la distribución de las ramas sigue cierto orden. Los árboles ordenados de grado 2 son de especial interés puesto que representan una de las estructuras de datos más importante en computación, conocida como árboles binarios. En un árbol binario cada nodo puede tener como máximo dos subárboles; y siempre es necesario distinguir entre el subárbol izquierdo y el subárbol derecho.
APLICACIONES DE ÁRBOLES BINARIOS:

• Árboles binarios de búsqueda.
• Representación de una expresión algebraica.
• Árbol Genealógico.

ÁRBOLES BINARIOS DISTINTOS: Dos árboles binarios son distintos cuando sus estructuras son diferentes. Ejemplo: A A B B A B A D B D C C.

ÁRBOLES BINARIOS SIMILARES: Dos árboles binarios son similares cuando sus estructuras son idénticas, pero la información que contienen sus nodos difiere entre sí. A E B C A F P S R J K T.

ÁRBOLES BINARIOS EQUIVALENTES: Los árboles binarios equivalentes se definen como aquellos que son similares y además los nodos contienen la misma información. E F J K E F J K.

ÁRBOLES BINARIOS COMPLETOS:  Se define un árbol binario completo como un árbol en el que todos sus nodos, excepto los de último nivel, tienen dos hijos; el subárbol izquierdo y el subárbol derecho. A B D C F GE.

RECORRIDOS EN ÁRBOLES BINARIOS: Una de las operaciones más importantes a realizar en un árbol binario es el recorrido de los mismos. Recorrer significa visitar los nodos del árbol en forma sistemática; de tal manera que todos los nodos del mismo sean visitados una sola vez. Existen tres formas diferentes de efectuar el recorrido y todas ellas de naturaleza recursiva, éstas son:

RECORRIDOS Recorrido en preorden: 

• Visitar la raíz 
• Recorrer el subárbol izquierdo
• Recorrer el subárbol derecho Recorrido en inorden:
• Recorrer el subárbol izquierdo 
• Visitar la raíz 
• Recorrer el subárbol derecho Recorrido en postorden: 
• Recorrer el subárbol izquierdo 
• Recorrer el subárbol derecho
• Visitar la raíz

ÁRBOL BINARIO DE BÚSQUEDA: El árbol binario de búsqueda es una estructura sobre la cual se pueden realizar eficientemente las operaciones de búsqueda, inserción y eliminación. Formalmente se define un árbol binario de búsqueda de la siguiente manera: “Para todo nodo T del árbol debe cumplirse que todos los valores de los nodos del subárbol izquierdo de T deben ser menores o iguales al valor del nodo T. De forma similar, todos los valores de los nodos el subárbol derecho de T deben ser mayores o iguales al valor del nodo T”.

Compuertas Lógicas - Álgebra Booleana

Álgebra Booleana 

Publicado por: Diego Valdez Martínez

Es una rama especial del álgebra que se usa principalmente en electrónica digital. El álgebra booleana fue inventada en el año 1854 por el matemático inglés George Boole.

El álgebra de Boole es un método para simplificar los circuitos lógicos (o a veces llamados circuitos de conmutación lógica) en electrónica digital.

Por lo tanto, también se llama como "Cambio de álgebra". Podemos representar el funcionamiento de los circuitos lógicos utilizando números, siguiendo algunas reglas, que son bien conocidas como "Leyes del álgebra de Boole".

También podemos hacer los cálculos y las operaciones lógicas de los circuitos aún más rápido siguiendo algunos teoremas, que se conocen como "Teoremas del álgebra de Boole". Una función booleana es una función que representa la relación entre la entrada y la salida de un circuito lógico.

La lógica booleana solo permite dos estados del circuito, como True y False. Estos dos estados están representados por 1 y 0, donde 1 representa el estado "Verdadero" y 0 representa el estado "Falso".

Leyes de Álgebra Booleana

• Leyes Conmutativas

 El orden en que se aplica a las variables la operación OR es indiferente:

 Ley conmutativa de la suma para dos variables

        A+B = B+A     

El orden en que se aplica a las variables la operación AND es indiferente:
Ley conmutativa de la multiplicación para dos variables

           AB = BA

• Leyes Asociativas

Al aplicar la operación OR a más de dos variables, el resultado es el mismo independientemente de la forma en que se agrupen las variables:
Ley asociativa de la suma para tres variables
     A + (B + C) = (A + B) + C

 
Al aplicar la operación AND a más de dos variables, el resultado es el mismo independientemente de la forma en que se agrupen las variables:
Ley asociativa de la multiplicación para tres variables

     A(BC) = (AB)C

• Ley Distributiva

Aplicar la operación OR a dos o más variables y luego aplicar la operación AND al resultado de la operación y  a otra variable aislada, es equivalente a aplicar la operación AND a la variable aislada con cada uno de los  sumandos y luego aplicar la operación OR a los productos resultantes.  Esta ley también expresa el proceso de sacar factor común, en el que la variable común se saca como factor  de los productos parciales 

Ley distributiva para tres variables 

         A (B + C) = AB + AC

Compuertas Logicas

Las puertas o compuertas lógicas básicas son: La puerta AND, la puerta OR y la puerta NOT. 

A continuación se presenta su símbolo, la tabla de verdad que nos dice la salida dependiendo de la combinación de las entradas y su ecuación lógica. 

• La puerta AND (Puerta Y) solo tiene una salida =1 o nivel alto si fuera un voltaje si ambas entradas son 1. 

• La puerta OR (puerta O) tiene una salida =1 si cualquiera o ambas de las entradas es 1. 

• La puerta NOT o Inversor niega la entrada, esto es, si la entrada es 0 la salida es 1 y si es 1 la salida es 0.

• La puerta NAND esta compuerta trabaja al contrario de una AND ya que al no tener entradas en 1 o solamente alguna de ellas, esta concede un 1 en su salida, pero si esta tiene todas sus entradas en 1 la salida se presenta con un 0.

• La puerta NOR la compuerta OR también tiene su versión inversa. Esta compuerta cuando tiene sus entradas en estado 0 su salida estará en 1, pero si alguna de sus entradas pasa a un estado 1 sin importar en qué posición, su salida será un estado 0.

• La puerta XOR también llamada OR exclusiva, esta actúa como una suma binaria de un digito cada uno y el resultado de la suma seria la salida. Otra manera de verlo es que con valores de entrada igual el estado de salida es 0 y con valores de entrada diferente, la salida será 1.

Tablas de la verdad: Una tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor        de verdad de una proposición compuesta, para cada combinación de verdad que se   pueda asignar. Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921.

La tabla de los "valores de verdad", es usada en el ámbito de la lógica, para obtener la verdad (V) o falsedad (F), valores de verdad, de una expresión o de una proposición. Además sirven para determinar si es que un determinado esquema de inferencia es formalmente válido como un argumento, llegando a la conclusión de que este es una tautología (se habla de una tautología cuando todos los valores de la tabla mencionada son "V" o sea verdadero).

Para establecer un Sistema formal se establecen las definiciones de los operadores. Las definiciones se harán en función del fin que se pretenda al construir el sistema que haga posible la formalización de argumentos:

·         Como razonamientos deductivos lógico-lingüísticos

·         Como construcción de un sistema matemático puro

·         Como una aplicación lógica en un Circuito de conmutación.

• Verdadero: El valor verdadero se representa con la letra V; si se emplea notación numérica se expresa con un uno: 1; en un circuito eléctrico, el circuito está cerrado.

• Falso: El valor falso se representa con la letra F; si se emplea notación numérica se expresa con un cero: 0; en un circuito eléctrico, el circuito está abierto.

• Variable: Para una variable lógica A, B, C,... que pueden ser verdaderas V, o falsas F, los operadores fundamentales se definen así:

• Negación: La negación es un operador que se ejecuta, sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.

• Conjunción: La conjunción es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir es verdadera cuando ambas son verdaderas.

• Las Disyunción: La disyunción es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.

• Implicación o Condicional: El condicional material es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de falso sólo cuando la primera proposición es verdadera y la segunda falsa, y verdadero en cualquier otro caso.

• Equivalencia, doble implicación o Bicondicional: El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad son diferentes.

Mapa de Karnaugh

Los Mapas de Karnaugh son una herramienta muy utilizada para la simplificación de circuitos lógicos. Cuando se tiene una función lógica con su tabla de verdad y se desea implementar esa función de la manera más económica posible se utiliza este método.
El mapa de Karnaugh es una herramienta muy útil para la simplificación y minimización de expresiones algebraicas Booleanas. Es similar a una tabla de verdad, ya que muestra todos los posibles valores de las variables de entrada y la salida resultante para cada valor.
Es una secuencia de celdas en la que cada celda representa un valor binario de las variables de entrada. El número de celdas de un mapa de Karnaugh es igual al número total de combinaciones de las variables de entrada, al igual que el número de filas para una tabla de verdad, es decir, si un mapa tiene 3 variables, (2) elevado a la 3 = 8.
Las celdas del mapa K se marcan de modo que las celdas horizontalmente y verticalmente adyacentes, solo difieran en una variable.
Vamos a definir algunos términos que nos son de mucha utilidad al momento de analizar los mapas K:

• Implicante: Un grupo de unos ó ceros adyacentes que implican a una variable en cuestión, agrupados en potencias de a dos.
• Adyacencia: Característica de un mapa K en el que sólo se cambia una variable de una celda a otra inmediata a ella por cualquiera de sus cuatro lados.

Mapa de Karnaugh de dos variables

El mapa de Karnaugh de dos variables es un conjunto de cuatro celdas.La siguiente figura nos muestra la tabla de verdad y el mapa K para una función escogida arbitrariamente de dos variables.

Mapa de Karnaugh de tres variables
El mapa de Karnaugh de tres variables es un conjunto de ocho celdas.La siguiente figura nos muestra la tabla de verdad y el mapa K para una funcíon escogida arbitrariamente de tres variables.

Aplicación de las compuertas lógicas

En el siguiente video se mostrara la aplicacion de las compuertas logicas en la electronica digital, mapas de karnaugh y las tablas de verdad.
Estas nos ayudaran para la creacion de un circuito electronico que se le sera aplicado a un semaforo.

Este ejemplo nos facilitara el uso de las tablas de verdad y los mapas de karnaugh, para asi entender mejor estas herramientas y poderlas aplicar en los circuitos que crearemos.